機械学習用の元データを作る
- 解説
- 1. 教師あり学習で回帰分析
- 2. 学習用教師データの作成
- 3. pandasを使った列どうしの計算
- 4. 特徴の組み合わせに対するラベルの作成
解説
1. 教師あり学習で回帰分析
さて、このカリキュラムの本題である「機械学習とその予測」について考えてみましょう。
ここまで、Pythonやpandasの使い方、データの分析方法など、機械学習の前提となる基礎に触れながら、「サイコロを振る」という現実世界の行動をコンピューター上で再現してその結果を分析できるようになりました。
これで、目の最大値が6のサイコロを1万回振った場合の平均値は3.5、7の場合4.0、8の場合4.5、9・10・11・・・と試行を繰り返して行けば、目の最大値が1増えた場合の平均値の増分が見えてきて、目の最大値が24の場合に平均値がいくつになるのかなど、予測ができそうですね。
機械学習も基本的にはこの流れと変わりありません。「目の最大値と平均値」のデータを与えると、以下のように学習していきます。(実際とは異なります)
(a)目の最大値が6・7・8のデータから平均値の増分を仮で算出
(b)aを元に9の場合の結果を予測してみて、実際の結果データと比較
(c)bのズレと、10・11・12のデータから平均値の増分を仮で算出
(d)cを元に13の場合の結果を予測してみて実際の結果と比較
これを繰り返すことで目の最大値と平均値の相関関係を学習し、目の最大値を与えるだけで平均値が予測できるようになるのです。
機械学習の世界では「目の最大値」のことを特徴と呼び、「サイコロを1万回振った場合の平均値」のことをラベルと呼びます。
4輪・大きいなら自動車、2輪・大きいならバイク、2輪・小さいなら自転車・・・というデータを学習していれば、写真から種類を予測して仕分けすることできます。これを分類といいます。特徴とラベルの呼び方は、分類だとしっくり来ますね。
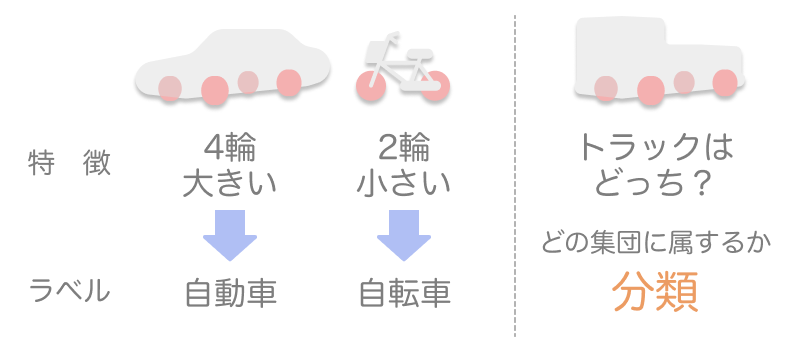
一方、前述のサイコロの例のように、連続性のある条件と値の相関関係から学習データにない条件に対応する値を予測することを回帰分析といいます。この場合も条件を特徴、対応する値をラベルと呼ぶので、慣れておきましょう。
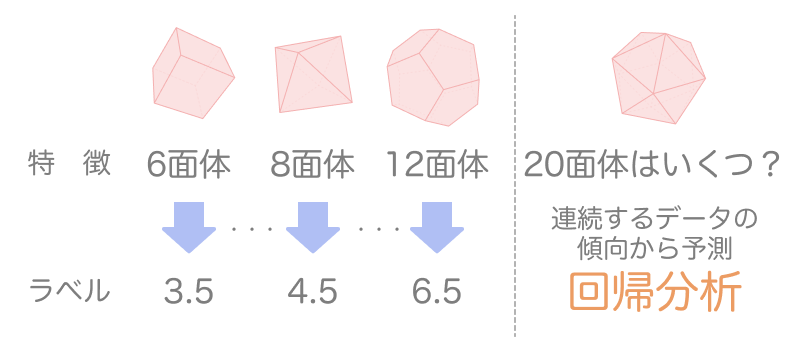
特徴とラベルの組み合わせを与える学習方法を「教師あり学習」と呼びます。このカリキュラムでは教師あり学習を使って、目の最大値が学習データの範囲を超えて増加していった場合の平均値の値を予測する回帰分析を行う、ということになります。
2. 学習用教師データの作成
学習させる教師データを作成していきますが、特徴が「サイコロ1つの目の最大値」だけでは単純すぎますので、サイコロを2つに増やしましょう。最大値の変化幅をそれぞれ1〜6(「サイコロ 面体」で検索してみましょう。)とすると「サイコロAの最大値が3、サイコロBの最大値が6」のような特徴の組み合わせが 6 x 6 = 36 通りとなります。
| (1) | Colab上で「step05.ipynb」を新規作成してください。 |
| (2) | 下記のコードをそれぞれ新しいセルに入力して、 「ランタイム」 > 「すべてのセルを実行」してください。 |
# インポート
import random
import pandas as pd
# 定数
DICE_A = 'サイコロA'
DICE_B = 'サイコロB'
DICE_AB = 'サイコロA/B'
DICE_MIN = 1
DICE_MAX = 6
ROLLS = 10
C_DICE_A = 'diceA'
C_DICE_B = 'diceB'
C_DICE_A_add_B = 'diceA+B'
C_ROLL_A_add_B = 'rollA+B'
C_ROLLS_A_add_B_SUM = 'rollsA+B_sum'
C_ROLLS_A_add_B_MEAN = 'rollsA+B_mean'# 「サイコロを振る」のと同じ状態を再現する関数
# 引数1つ目はint型、dice_max=サイコロの最大値
# 引数2つ目はint型、dice_min=サイコロの最小値、省略時は1
# 戻り値はint型、サイコロを振った結果の目の値
def roll_dice(dice_max: int, dice_min: int = 1) -> int:
return random.randint(dice_min, dice_max)# DICE_MIN/DICE_MAX の範囲内の目の最大値を持つ
# サイコロA/Bすべて組合せの配列(pandas.DataFrame)を生成する
dice_df = pd.DataFrame([[diceA_max, diceB_max]
for diceA_max in range(DICE_MIN, DICE_MAX + 1)
for diceB_max in range(DICE_MIN, DICE_MAX + 1)
], columns=[C_DICE_A, C_DICE_B])
print('目の最大値が{}〜{}の{}の組合せ'.format(DICE_MIN, DICE_MAX, DICE_AB))
dice_df実行して次の結果が出力されればOKです。(実際は表形式で出力されますが、以降も同様に、簡略化して表示します。)
目の最大値が1〜6のサイコロA/Bの組合せ
diceA diceB
0 1 1
1 1 2
2 1 3
3 1 4
4 1 5
5 1 6
6 2 1
7 2 2
8 2 3
9 2 4
10 2 5
11 2 6
12 3 1
13 3 2
14 3 3
15 3 4
16 3 5
17 3 6
18 4 1
19 4 2
20 4 3
21 4 4
22 4 5
23 4 6
24 5 1
25 5 2
26 5 3
27 5 4
28 5 5
29 5 6
30 6 1
31 6 2
32 6 3
33 6 4
34 6 5
35 6 6ポイント
多次元配列
step05.ipynb - セル 3 ではリスト内包表記でデータを作成してDataFrameに渡していますが、3行目の最後(ひとつ目のforの左側)がさらに配列になっています。配列の要素がさらに配列になることを2次元配列といいます。出力結果を見ると、行が外側の配列で下方向に増えていき、その各行には内側の配列の値が格納されていることがわかります。2次元配列は表と捉えると良いでしょう。
for文の二重構造
diceA_maxはひとつ目のforで、diceB_maxはふたつ目のforで定義されています。出力結果を見るとdiceA_maxが1増える間にdiceB_maxは1〜6まで増えて、また1に戻っています。つまり、for文を2つ並べることで、二重ループを形成して組み合わせのパターンを網羅しています。
3. pandasを使った列どうしの計算
pandasでは列どうしで計算を行うと、各行の中身どうしを計算したことと同じになります。
| (1) | 下記のコードをそれぞれ新しいセルに入力して、 「ランタイム」 > 「すべてのセルを実行」してください。 |
# サイコロA/Bの最大値を加算した列を追加
# pandas.DataFrameならばfor文で行方向にループ処理しなくても列どうしの加算が可能
dice_df[C_DICE_A_add_B] = dice_df[C_DICE_A] + dice_df[C_DICE_B]
print('目の最大値が{}〜{}の{}の組合せ+目の最大値の加算列'.format(DICE_MIN, DICE_MAX, DICE_AB))
dice_df実行して次の結果が出力されればOKです。
目の最大値が1〜6のサイコロA/Bの組合せ+目の最大値の加算列
diceA diceB diceA+B
0 1 1 2
1 1 2 3
2 1 3 4
3 1 4 5
4 1 5 6
5 1 6 7
6 2 1 3
7 2 2 4
8 2 3 5
9 2 4 6
10 2 5 7
11 2 6 8
12 3 1 4
13 3 2 5
14 3 3 6
15 3 4 7
16 3 5 8
17 3 6 9
18 4 1 5
19 4 2 6
20 4 3 7
21 4 4 8
22 4 5 9
23 4 6 10
24 5 1 6
25 5 2 7
26 5 3 8
27 5 4 9
28 5 5 10
29 5 6 11
30 6 1 7
31 6 2 8
32 6 3 9
33 6 4 10
34 6 5 11
35 6 6 12右辺の列を加工することも可能です。
| (2) | 下記のコードをそれぞれ新しいセルに入力して、 「ランタイム」 > 「すべてのセルを実行」してください。 |
# サイコロの組合せごとにサイコロを振り、出た目を加算して列として追加
# サイコロ目の最大値の列毎にmapでループ処理を行い「サイコロを振った結果の配列」を作成し、
# 列どうしで加算してその結果を新たな列として追加している
dice_df[C_ROLL_A_add_B] = (
dice_df[C_DICE_A].map(lambda dice_max: roll_dice(dice_max)) +
dice_df[C_DICE_B].map(lambda dice_max: roll_dice(dice_max)))
print('{}を振って加算した結果の列を追加'.format(DICE_AB))
dice_df実行して次のような結果が出力されればOKです。
サイコロA/Bを振って加算した結果の列を追加
diceA diceB diceA+B rollA+B
0 1 1 2 2
1 1 2 3 3
2 1 3 4 2
3 1 4 5 2
4 1 5 6 4
5 1 6 7 4
6 2 1 3 2
7 2 2 4 4
8 2 3 5 2
9 2 4 6 3
10 2 5 7 2
11 2 6 8 3
12 3 1 4 3
13 3 2 5 3
14 3 3 6 2
15 3 4 7 3
16 3 5 8 5
17 3 6 9 3
18 4 1 5 3
19 4 2 6 5
20 4 3 7 3
21 4 4 8 5
22 4 5 9 7
23 4 6 10 6
24 5 1 6 5
25 5 2 7 2
26 5 3 8 7
27 5 4 9 4
28 5 5 10 3
29 5 6 11 8
30 6 1 7 6
31 6 2 8 5
32 6 3 9 3
33 6 4 10 5
34 6 5 11 6
35 6 6 12 9ポイント
DataFrameの列
pandas.DataFrameの変数名に「[](角括弧)」をつけて列名を渡すと、Series(シリーズ)という特別なオブジェクトになります。基本統計値の算出を行った際もこの方法で参照していましたね。このSeriesにはmean・median・modeなど以外にもたくさんの関数が備わっており、様々な集計や変換などの操作が可能です。
map
step05.ipynb - セル 5 の 5-6 行目 では、Seriesに対してmap(マップ)関数を適用しています。mapはSeriesに含まれる各項目(Seriesは列であるため、各行の値)に対して、ひとつ目の引数の関数を実行して値を変換できます。そのため、引数に渡す関数は引数の値を受け取りそれを加工して戻り値とする関数の形となります。
なお、mapはpythonの組み込み関数としても用意されており、使う場合には map(変換関数, 変換したい値の入った配列) の形式で呼び出します。
lambda
map(マップ)関数とlambda(ラムダ)はセット覚えましょう。lambdaは無名の関数をその場で定義するためのキーワードです。
本来、関数は「def 関数名(仮引数名:型名) -> 戻り値の型名:」という形式で定義する必要がありますが、lambdaキーワードの右側に仮引数名(無ければ無し、複数あればカンマつなぎ)を書き、コロンで区切って右側に関数の本体を書きます。
mapの引数などのように関数の引数として関数を渡したいなどの場合に便利な構文です。
4. 特徴の組み合わせに対するラベルの作成
これで特徴の組み合わせ(サイコロAとBの最大値の組み合わせ)に対して、様々な処理を簡単に行えるようになりましたので、対応するラベル(その組み合わせのサイコロを10回振った際の平均値)を列として追加しましょう。
| (1) | 下記のコードを新しいセルに入力して、 「ランタイム」 > 「すべてのセルを実行」してください。 |
# 前のセルで追加したサイコロ1回の列は削除しておく
dice_df = dice_df.drop(columns=C_ROLL_A_add_B)
# サイコロの組合せごとにサイコロを振り、出た目を加算、それをROLLS回行った平均を列として追加
# まずは合計列をゼロでクリアしておき、そこにROLLS回、出た目の加算結果を合計していく
dice_df[C_ROLLS_A_add_B_SUM] = 0
for _ in range(ROLLS):
dice_df[C_ROLLS_A_add_B_SUM] += (
dice_df[C_DICE_A].map(lambda dice_max: roll_dice(dice_max)) +
dice_df[C_DICE_B].map(lambda dice_max: roll_dice(dice_max)))
print('{}を振って加算した結果を{}回分合計した列を追加'.format(DICE_AB, ROLLS))
dice_df実行して次のような結果が出力されればOKです。
サイコロA/Bを振って加算した結果を10回分合計した列を追加
diceA diceB diceA+B rollsA+B_sum
0 1 1 2 20
1 1 2 3 25
2 1 3 4 30
3 1 4 5 38
4 1 5 6 36
5 1 6 7 47
6 2 1 3 27
7 2 2 4 27
8 2 3 5 35
9 2 4 6 37
10 2 5 7 44
11 2 6 8 54
12 3 1 4 37
13 3 2 5 33
14 3 3 6 45
15 3 4 7 40
16 3 5 8 54
17 3 6 9 58
18 4 1 5 40
19 4 2 6 42
20 4 3 7 46
21 4 4 8 53
22 4 5 9 52
23 4 6 10 45
24 5 1 6 31
25 5 2 7 39
26 5 3 8 49
27 5 4 9 58
28 5 5 10 58
29 5 6 11 76
30 6 1 7 37
31 6 2 8 40
32 6 3 9 55
33 6 4 10 65
34 6 5 11 66
35 6 6 12 65このままではただの合計値ですので、平均を算出しましょう。
| (2) | 下記のコードを新しいセルに入力して、 「ランタイム」 > 「すべてのセルを実行」してください。 |
# 合計した列をROLLSで割って平均列として追加
dice_df[C_ROLLS_A_add_B_MEAN] = dice_df[C_ROLLS_A_add_B_SUM] / ROLLS
print('{}を振って加算した結果の{}回分合計を平均した列を追加'.format(DICE_AB, ROLLS))
dice_df実行して次のような結果が出力されればOKです。
サイコロA/Bを振って加算した結果の10回分合計を平均した列を追加
diceA diceB diceA+B rollsA+B_sum rollsA+B_mean
0 1 1 2 20 2.0
1 1 2 3 25 2.5
2 1 3 4 30 3.0
3 1 4 5 38 3.8
4 1 5 6 36 3.6
5 1 6 7 47 4.7
6 2 1 3 27 2.7
7 2 2 4 27 2.7
8 2 3 5 35 3.5
9 2 4 6 37 3.7
10 2 5 7 44 4.4
11 2 6 8 54 5.4
12 3 1 4 37 3.7
13 3 2 5 33 3.3
14 3 3 6 45 4.5
15 3 4 7 40 4.0
16 3 5 8 54 5.4
17 3 6 9 58 5.8
18 4 1 5 40 4.0
19 4 2 6 42 4.2
20 4 3 7 46 4.6
21 4 4 8 53 5.3
22 4 5 9 52 5.2
23 4 6 10 45 4.5
24 5 1 6 31 3.1
25 5 2 7 39 3.9
26 5 3 8 49 4.9
27 5 4 9 58 5.8
28 5 5 10 58 5.8
29 5 6 11 76 7.6
30 6 1 7 37 3.7
31 6 2 8 40 4.0
32 6 3 9 55 5.5
33 6 4 10 65 6.5
34 6 5 11 66 6.6
35 6 6 12 65 6.5ポイント
計算の単純化
セル6では、前項で示したセル5の計算方法をそのままに、単純に10回「+=」で加算する方式としています。また、セル7では平均を別の列として算出しています。
慣れるまではなるべく計算は単純化して、列を増やして視覚的に計算の段階を確認できるようにしましょう。
改行でエラー?
プログラムコードの複雑化に伴い、だんだんと長い行が増えてきました。セル5の7行目なんかも「+=」の右側で改行したくなりますが、残念ながら構文エラーになってしまいます。
Pythonは改行の位置に厳しいです。ただし、丸括弧の中では比較的自由度が上がりますので、このようなケースでは「+= (」の右側で改行すると、エラーになりません。見やすいように適宜改行を工夫しましょう。
ただし、関数やfor文の範囲は左からの開始位置(インデント)で表現しますので、改行後にインデントが崩れないように十分注意しましょう。
問題
確認問題
確認問題1
以下に挙げる「機械学習による分類」の活用例と、その「教師データの特徴とラベル」の組み合わせのうち、正しい結果が得られないと考えられる組み合わせはどれか?
確認問題2
以下に挙げる「機械学習の活用例」が分類であるか回帰分析であるか、正しくない組み合わせはどれか?
確認問題3
この中で多次元配列の定義とその参照の正しくない組み合わせはどれか?
確認問題4
この中でmapとlambdaを使用した処理とその結果の正しい組み合わせはどれか?
実践問題
問題
step05.ipynbの末尾に新しいセルを追加し、セル6と7を参考に必要なコードを入力して、サイコロA/Bを振って乗算した結果の10回分合計を平均した列を追加してください。
なお、最終的に次の結果例と同等の処理結果が確認できれば良く、追加するセルの数は問いません。また、定数の定義も先頭ではなく追加したセル内で行って構いません。

