グラフ化する
- 解説
- 1. 関数化する
- 2. 2次元グラフにプロットする
- 3. 2次元グラフの傾きを明確にする
- 4. 3次元グラフにプロットする
解説
1. 関数化する
学習用の教師データができましたが、データの計算処理が進み、表形式だけでは内容を把握しきれなくなってきましたので、グラフにして見てみましょう。まずは複雑化してきたここまでの計算をコンパクトに関数化していきます。
| (1) | Colab上で「step06.ipynb」を新規作成してください。 |
| (2) | 下記のコードをそれぞれ新しいセルに入力して、 「ランタイム」 > 「すべてのセルを実行」してください。 |
# インポート
import random
import pandas as pd
import altair as alt
import plotly.express as px
# 定数
DICE_AB='サイコロA/B'
DICE_MIN = 2
DICE_MAX = 20
ROLLS=100
C_DICE_A='diceA'
C_DICE_B='diceB'
C_DICE_A_add_B='diceA+B'
C_ROLLS_A_add_B_MEAN='rollsA+B_mean'# 「サイコロを振る」のと同じ状態を再現する関数
# 引数1つ目はint型、dice_max=サイコロの最大値
# 引数2つ目はint型、dice_min=サイコロの最小値、省略時は1
# 戻り値はint型、サイコロを振った結果の目の値
def roll_dice(dice_max: int, dice_min: int = 1) -> int:
return random.randint(dice_min, dice_max)# step05のコードを簡略化して関数化
def create_dice_df(dice_min: int, dice_max: int, rolls: int) -> pd.DataFrame:
dice_df = pd.DataFrame([[diceA_max, diceB_max]
for diceA_max in range(dice_min, dice_max + 1)
for diceB_max in range(dice_min, dice_max + 1)
], columns=[C_DICE_A, C_DICE_B])
dice_df[C_DICE_A_add_B] = dice_df[C_DICE_A] + dice_df[C_DICE_B]
# 仮合計列は列名も仮の0で良い
dice_df[0] = 0
for _ in range(rolls):
# lambdaに続く引数の数と型が同じ関数ならば、関数を直接mapの引数に指定できる
dice_df[0] += (dice_df[C_DICE_A].map(roll_dice)
+ dice_df[C_DICE_B].map(roll_dice))
dice_df[C_ROLLS_A_add_B_MEAN] = dice_df[0] / rolls
# 仮合計列は削除してしまう
dice_df.pop(0)
return dice_df# step05と同じデータを作成
dice_df = create_dice_df(DICE_MIN, DICE_MAX, ROLLS)
print('{}を{}回振って合計を平均'.format(DICE_AB, ROLLS))
dice_df実行して次の結果が出力されればOKです。
サイコロA/Bを100回振って合計を平均
diceA diceB diceA+B rollsA+B_mean
0 2 2 4 3.13
1 2 3 5 3.46
2 2 4 6 3.76
3 2 5 7 4.47
4 2 6 8 5.04
.. ... ... ... ...
356 20 16 36 17.85
357 20 17 37 19.52
358 20 18 38 19.50
359 20 19 39 19.28
360 20 20 40 20.212. 2次元グラフにプロットする
教師データを2次元グラフに点グラフとして表示してみましょう。グラフにデータを反映することをプロットと呼びます。
前項の出力結果の通り、2から20の目を持つサイコロA/Bの組み合わせ(厳密には順列)は361パターンです。そのパターン毎に100回サイコロを振った平均値となっていますので、表示される点は361個ということになります。
| (1) | 下記のコードを新しいセルに入力して、 「ランタイム」 > 「すべてのセルを実行」してください。 |
# 2dグラフ化
scatter_graph = alt.Chart(dice_df).mark_circle(size=40, color='rgba(255,0,0,0.5)').encode(
x=alt.X(
C_DICE_A_add_B,
axis=alt.Axis(title='{}の目の最大値合算'.format(DICE_AB))),
y=alt.Y(
C_ROLLS_A_add_B_MEAN,
axis=alt.Axis(title='{}回振った平均値'.format(ROLLS)))
).properties(
width=500,
height=400,
title='サイコロの組合せと{}回振った平均値(2D)'.format(ROLLS)
).interactive()
# 表示
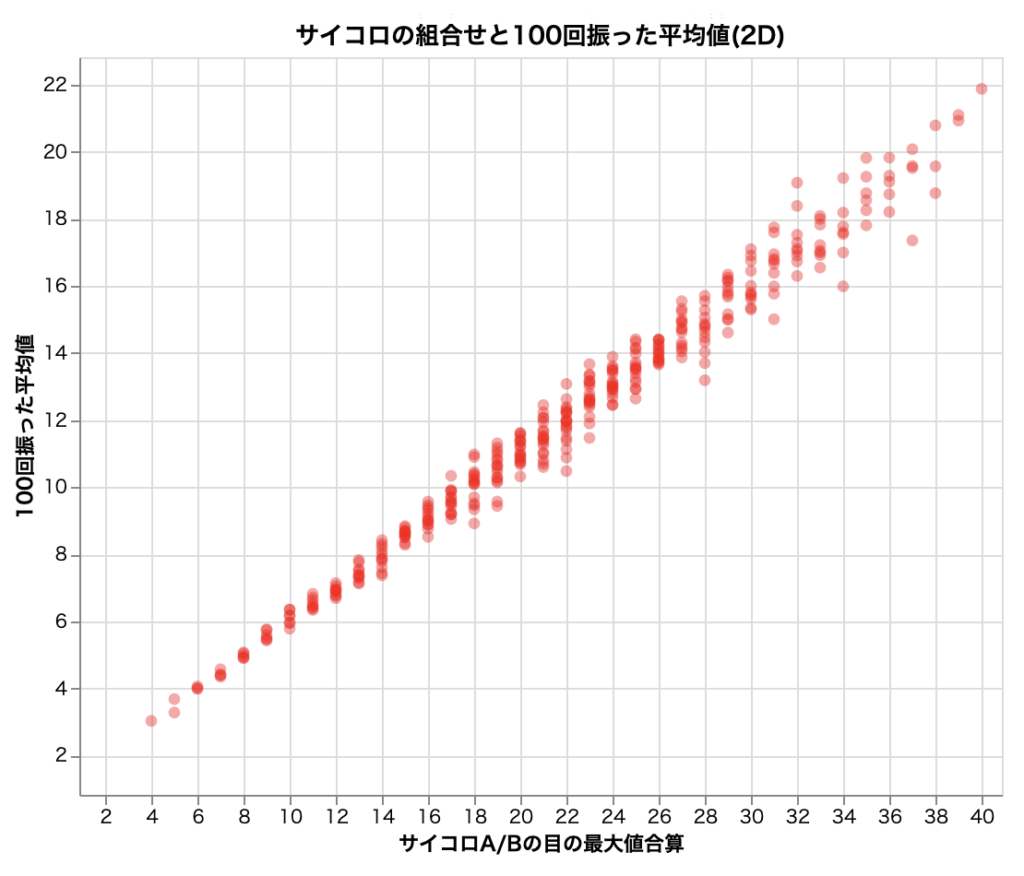
scatter_graph実行して次の結果が出力されればOKです。
ポイント
グラフ生成ライブラリ:altair
この2次元(2D=2-Dimensions)グラフには、altair(アルタイル)というライブラリを使用しています。グラフの上でマウスホイールを操作するとズーム、ドラッグすると座標表示範囲を移動することができます。また、右上の「・・・」ボタンからは、画像として保存することが可能です。
altairは、他の教材やサイトでよく使われているグラフ生成ライブラリではできない機能が色々ありますので、こちらを使うことに慣れておきましょう。
グラフ生成コードの構成
altairによってグラフを生成するには、以下のように設定を行います。
・alt.Chartによってdice_dfのグラフのベースを作成
・mark_circleでプロットするポイントの大きさや色を指定
・encodeで掛け合わせる横=xと縦=yの軸(axis)のデータ列やタイトルを指定
・propertiesで表全体の大きさやタイトルを指定
・interactiveでズームや座標範囲移動を可能化
その他にもいろいろな設定が可能ですので、以下のURLを見ておきましょう。
https://altair-viz.github.io/gallery/index.html
グラフの軸
生成されたグラフの軸に注目してみましょう。横方向に伸びる軸には「サイコロA/Bの目の最大値合算」とあり、縦方向に伸びる軸には「100回振った平均値」とあります。つまり、2つのサイコロの最大値を足した値が増えるに従って、そのサイコロを振った目の合計値が右肩上がりに増えていく、という相関関係が見えてきます。
一見すると当たり前のことを確認しているようではありますが、視覚的にも確認しておくことは、扱うデータが複雑化していくと大変重要になります。また、データの散らばり具合であったり、密集度など、表で見ていてもあまり目に付かないポイントも見えてきますので、積極的にグラフ化するようにしましょう。
3. 2次元グラフの傾きを明確にする
グラフ化したことで、2つのサイコロの最大値を足した値が増えるに従って、そのサイコロを振った目の合計値が右肩上がりに増えていく、という相関関係が見えてきました。
線グラフであればそれを傾きとして明確に表現できるのですが、今は点の重なり具合などによりぼやけています。一見真っ直ぐだと言い切ってしまっても良さそうですが、ズームするとまた違った分布になっているようにも見えます。
そこで、このグラフの中心線を表現してみましょう。
グラフの点の数は361個ですが、左下の端(横軸=4)は サイコロA=2 + サイコロB=2 のひとつだけで、同様に右上の端(横軸=40)も 20 + 20 のみとなります。反対に一番多いのは横軸が22となる場合で、19個の点=サイコロの組み合わせが存在します。
つまり、横軸毎に1〜19個ずつ存在する各点の縦軸の値の平均を繋いでいけば、中心線となりそうです。
| (1) | 下記のコードを新しいセルに入力して、 「ランタイム」 > 「すべてのセルを実行」してください。 |
# 2dグラフに平均値を表示
# 「サイコロA/Bの目の最大値合算」ごとに合計して、その平均値を算出
dice_df_mean = (dice_df.groupby(C_DICE_A_add_B, as_index=False)
.agg({ C_ROLLS_A_add_B_MEAN: 'mean' }))
# 線グラフ
line_graph = alt.Chart(dice_df_mean).mark_line(color='rgba(255,0,0,1)').encode(
x=C_DICE_A_add_B,
y=C_ROLLS_A_add_B_MEAN)
# 2つのグラフを合体して表示
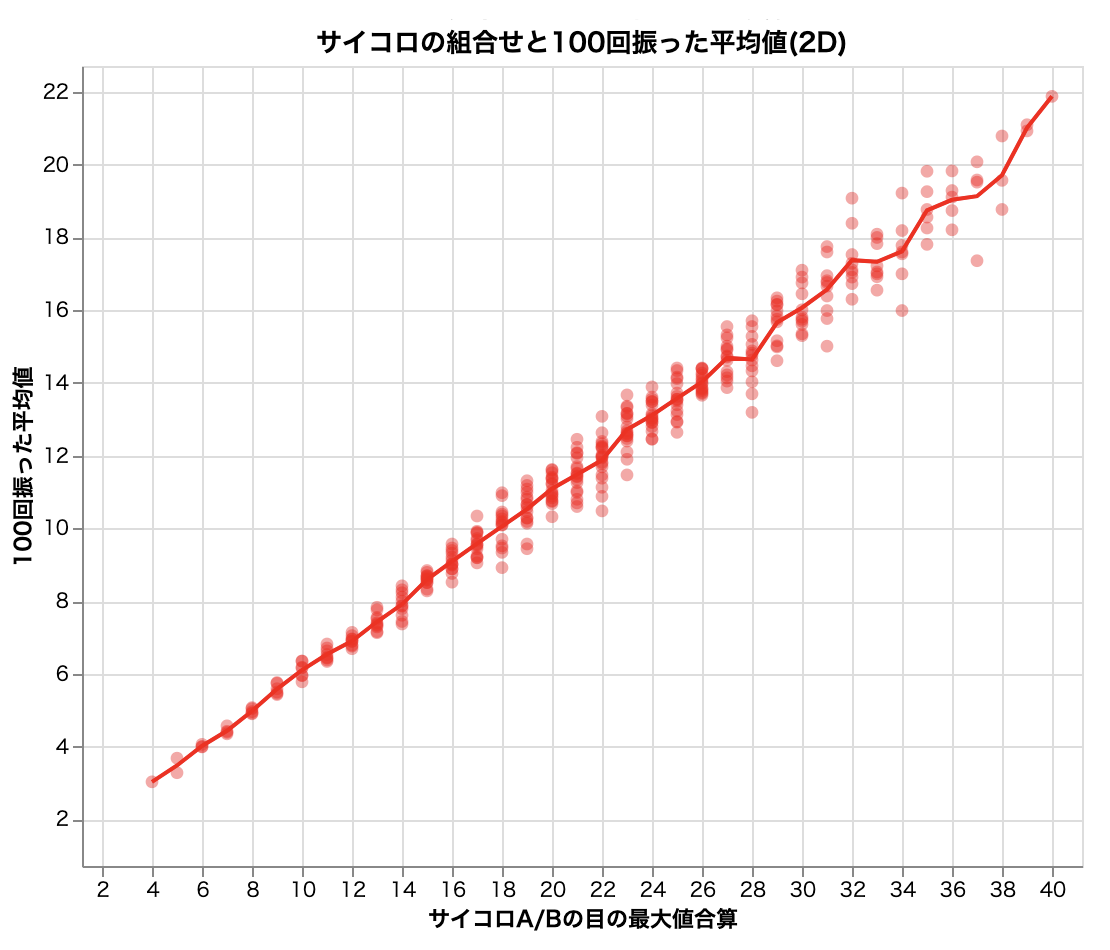
scatter_graph + line_graph実行して次の結果が出力されればOKです。
ポイント
DataFrame.groupby / .agg
中心線表示用のデータ作成には、pandas.DataFrameのgroupbyとaggという集計関数を使用しています。
groupbyはSQLを触ったことがある人ならイメージが湧くと思いますが、同じ値でグルーピングする関数です。引数に指定している C_DICE_A_add_B の値が同じデータをグループ化、つまり、横軸が22の時には19個のデータがひとまとめにされるということです。ひとまとめにしただけでは、グラフに何を表示すべきかわかりません。そこで、aggの出番です。
aggはaggregate=集計の略です。引数には C_ROLLS_A_add_B_MEAN を mean するよう指定しています。つまり、groupbyによってひとまとめになったデータの縦軸の値の平均値をそのグループの値として置き換えているのです。
わかりにくければ、dice_df_meanもこれまでのように画面に表示させてみましょう。
グラフの傾きと線形グラフ
生成された赤い線グラフの傾きに注目してみましょう。
簡単のために軸が交差している箇所だけ抜き出すと、横軸が6の時に縦軸が4、10の時6、14の時8、というようになっています。横軸が2増える毎に縦軸は1増える、つまり傾きは0.5となり、ここまでを数式で表すと y = 0.5x となります。
また、このグラフを伸ばして横軸が0の時を想像すると、縦軸は0より上の位置にありそうです。右辺にxを当てはめて計算してみると、6 x 0.5 = 3、10 x 0.5 = 5、14 x 0.5 = 7、のように縦軸の値より1少ないようです。つまり、すべての縦軸の値は +1 されているようです。これをグラフの切片(せっぺん)と言います。
最終的にこれを数式で表すと、y = 0.5x + 1となり、真っ直ぐな線形グラフであると言えそうです。
サンプルサイズとばらつきと誤差
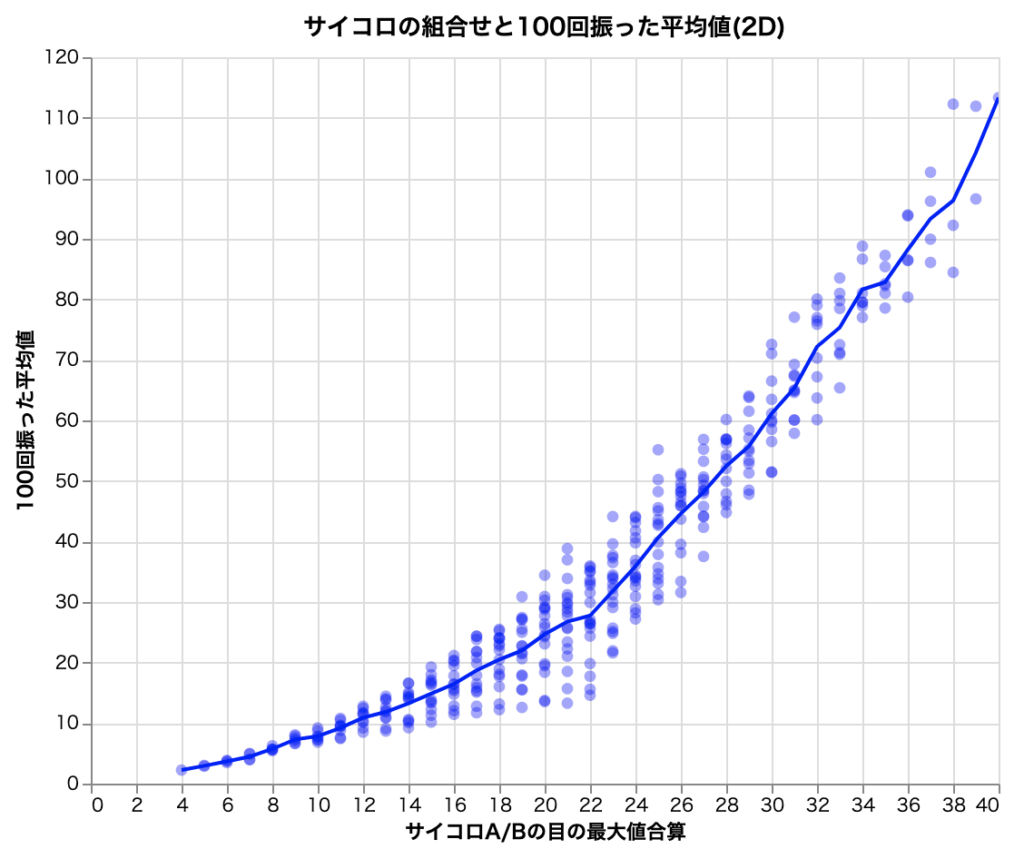
もしも「右上の方は線形じゃない・・・」と納得が行かないならば、DICE_MAXを倍の40にして再度実行してみてください。点の数が1521まで増え、グラフの範囲も右上に伸びました。
このグラフで先ほどの右上、つまり横軸が40のあたりをみると、先ほどの数式が綺麗に当てはまりそうですね。でもやはり、今のグラフの右上ではばらつきが見られます。平均からの距離を誤差と呼び、誤差の大きいデータが目立つ状態は一般的にばらつきと呼ばれます。
左下は、サンプルサイズ(点の数)が少ないですが、そもそもサイコロの目の最大値が小さく、取りうる値の範囲が小さいため誤差が小さいです。
真ん中あたりは、サンプルサイズが多くなっているため、平均値が想定通り算出できています。
右上は、サンプルサイズが少なく、サイコロの目の最大値も大きいため、誤差の大きさが平均に影響しやすくなってしまうのです。
4. 3次元グラフにプロットする
ここで、横軸についてあらためて考えてみると、「サイコロの目の最大値の組み合わせ」だったはずなのに合算してしまっています。これでは、特徴を増やした意味がありません。3次元グラフにして、軸をサイコロAとサイコロBに分割しましょう。
| (1) | 下記のコードを新しいセルに入力して、 「ランタイム」 > 「すべてのセルを実行」してください。 |
# 3dグラフ化
scatter_graph3d = px.scatter_3d(
dice_df,
x=C_DICE_A,
y=C_DICE_B,
z=C_ROLLS_A_add_B_MEAN,
color_discrete_sequence=['rgba(255,0,0,0.5)'])
scatter_graph3d.update_traces(marker_size = 2)
scatter_graph3d.update_layout(
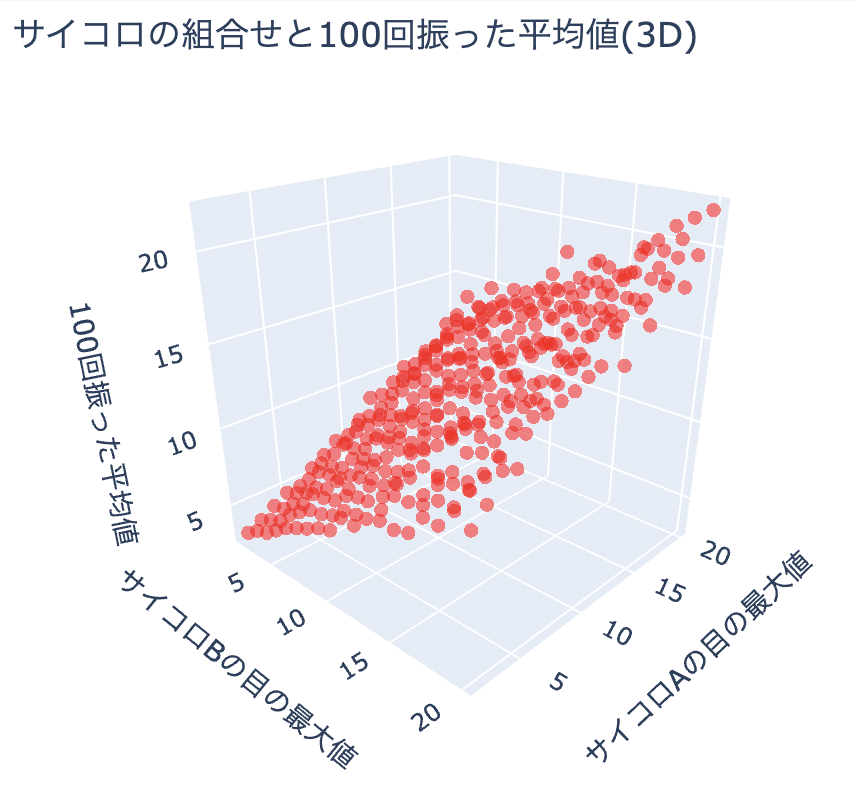
title='サイコロの組合せと{}回振った平均値(3D)'.format(ROLLS),
scene=dict(
xaxis=dict(title='サイコロBの目の最大値'),
yaxis=dict(title='サイコロAの目の最大値'),
zaxis=dict(title='{}回振った平均値'.format(ROLLS))),
margin=dict(l=0, r=0, b=0, t=30),
scene_camera=dict(
eye=dict(x=1.6, y=-1.7, z=1),
center=dict(x=0, y=0, z=-0.2)),
width=500,
height=400,
autosize=False)
scatter_graph3d.show()実行して次の結果が出力されればOKです。
ポイント
グラフ生成ライブラリ:plotly.express
この3Dグラフには、plotly.expressというライブラリを使用しています。こちらもグラフの上でマウスホイールを操作するとズーム、ドラッグするとぐるぐると回すことができます。
グラフ生成コードの構成
plotly.expressによってグラフを生成するには、以下のように設定を行います。
・px.scatter_3dによってdice_dfのグラフのベースを作成し各軸(x,y,z)と色を指定
・update_tracesでプロットするポイントの大きさを指定
・update_layoutで表全体の大きさやタイトルを指定
・scene_cameraで初期表示時の回転や視点距離を指定
その他にもいろいろな設定が可能ですので、以下のURLを見ておきましょう。
https://plotly.com/python/plotly-express/
4次元は無い
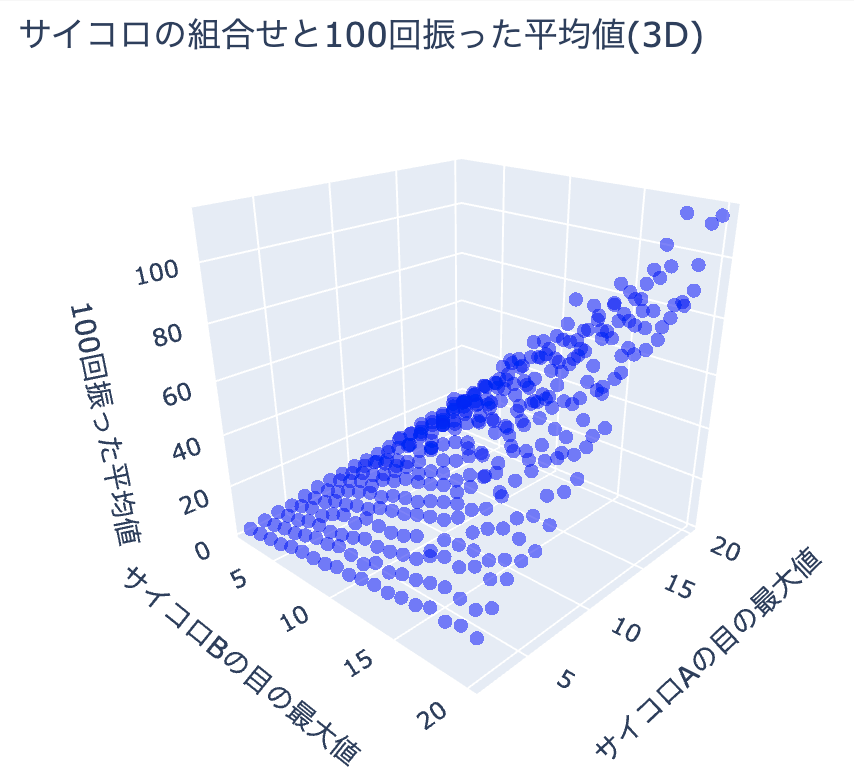
生成されたグラフの軸に注目してみましょう。左奥から中央手前方向に伸びる軸には「サイコロBの目の最大値」とあり、中央手前から右奥方向に伸びる軸には「サイコロAの目の最大値」とあります。そして、2Dの時と同じく、縦方向に伸びる軸には「100回振った平均値」とあります。
グラフにプロットされた点は右上に傾いた平行四辺形の形に見えますね。グラフの中央手前あたりをドラッグして、マウスを少し上に移動すると、2Dのグラフと同じように見えると思います。合算していたため線状に見えていましたが、分解するとこのような拡がりを持っていたということがわかります。
今回は2Dを3Dにすることでより詳しくみることができましたが、4D以降はあり得ません。さらにデータの次元数が増えた場合には、データを分割したり一部を取り出したりして、2Dまたは3Dに表現することで、データの把握に役立てましょう。
問題
実践問題
問題
step06.ipynbの各セルに必要なコードを入力して、グラフの点や線の色を変更してください。また、セル3のcreate_dice_df関数内12〜13行目で行っている処理を加算「+」から乗算「*」に変更して、その結果をグラフで確認してください。
なお、
rgba(255, 0, 0, 1) => 赤100%、不透明度100%
rgba(0, 255, 0, 1) => 緑100%、不透明度100%
rgba(0, 0, 255, 1) => 青100%、不透明度100%
rgba(255, 0, 0, 0.5) => 赤100%、不透明度50%
rgba(255, 0, 0, 0.5) => 赤100%、不透明度50%
※ r=red / g=green / b=blue は各色の比率を 0〜255 の範囲で表現
※ a=alpha は不透明度を 0〜1 の範囲で表現、0ならば透明
正解は省略します。